The standard model of measuring efficacy as a function of receptor occupancy was deemed to be insufficient to adequately explain the dose-response relationships often observed, that were steeper than those predicted by the law of mass action; or why sometimes a supra maximal drug concentration failed to elicit a maximal response within previously observed systems. This was predominantly manifested by a lack of a linear correlation, as predicted by the hyperbolic Langmuir isotherm, between the observed responses of a ligand on its tissues versus the fractions of occupied receptors. In 1956, R. P. Stephenson argued that the magnitude of response, in a tissue, to a given stimulus was the product of the intrinsic efficacy 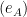 of the agonist and the fractions of occupied receptors,
of the agonist and the fractions of occupied receptors, 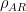 , as defined by the Hill-Langmuir equation: Continue reading →
, as defined by the Hill-Langmuir equation: Continue reading →
 When applying the law of mass action to these simultaneous equations, we can derive the following relationship: Continue reading
When applying the law of mass action to these simultaneous equations, we can derive the following relationship: Continue reading 


